SINGULAR POINTS IN THE SOLAR CHROMOSPHERE
M.M.Molodensky and L.I.Starkova
In the structure of the solar chromosphere, containing information on the configuration of the magnetic field, we have found and identified all the main types of the singular points ( see Fig. 1 ), which are known as inherent features of the 2-D vector field.

Fig.1. The types of singular points of the 2-D vector field. The main types of the singular points are the node, the focus, the center, and the saddle. They are shown in Fig.1.
The characteristic feature of the solar chromosphere is it's fibre structure. Near horizontal fibrils, which are parallel to the magnetic field, cover all the sun surface. The arrangement of the fibrils resembles the one of the iron filings in the magnetic field. The magnetic fields of the spots and the filament electrical currents can make the fibrils to trace the curves, which are characteristic of the neighbourhood of the node, the focus, the center, or the saddle (see Fig.2-4). Every type of the singular points can be related to the well-established chromospheric structure. Arrangement of the singular points roughly defines the behaviour of the integral curves of the vector field. Thus, investigation of the chromospheric magnetic field reduces to the study of the behaviour of the integral curves in the vicinity of the singular points, that is to application of the specific section of the the theory of ordinary differential equations, - the theory of vector field rotation (the theory of the indexes).
An analogy between the chromospheric structures and the singular points of the vector field let not only investigate the topological features, but also calculate some magnetic and electrical magnitudes.
The singular points of the node (the focus) type are known among the chromospheric formations as the rosettes. They are associated with extrema of the magnetic field potential, the sunspots and the magnetic hills.

Fig.2. Singular point of the focus type in the solar chromosphere. The H-alpha fibril structure around a simple sunspot near disk center creates a singular point of the focus type. [ Copyright C 1974 by R.J.Bray and R.E.Loughhead ].
The structure of the direction field characterize the vicinity of the node (the focus). This knowledge can be used to obtain a number of integral characteristics in the case of the well developed single unipolar sunspot, e.g. the relation of the magnetic field magnitude to the electric current an the dipole and quadrupole moments.
The next type of the singular points is the saddle. The number and arrangement of the saddle points are defined by the number and arrangement of the sunspots. The limiting lines, separating the the magnetic fluxes of the opposite directions pass through the chromospheric saddle points. It follows from the theorem about the vector field index, that the number of saddles in the plane is one less than the total number of nodes and focuses.
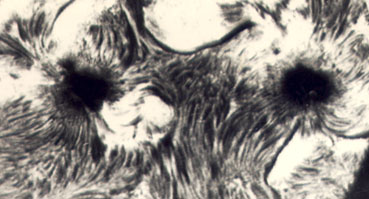
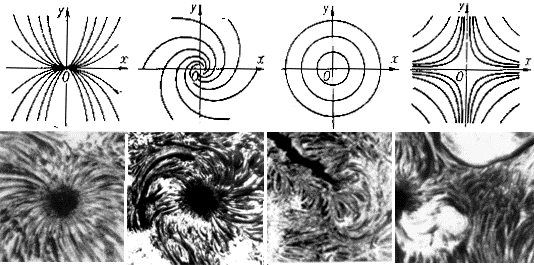
Fig.3. Singular point of the chromospheric saddle type. The two sunspots, looking like the nodes, create a saddle point in the plane of chromosphere. [ Fig.3 is presented by the courtesy of E.I.Mogilevsky, IZMIRAN, Russia ].
Singular points of the center type are observed near the spots and near the ends of the sharply scratched filaments. In the first case, the singular points form a node-saddle-center group, and in the latter one we observe an isolated singular point. The structures of the focus type can be found among the sunspots having a well-developed superpenumbra with an azimutal field. A pair of singular points can generate a saddle point. We observed such an association of three singular points in a sunspot of June 3, 1973 ( see the next picture, in which we show the tangential field lines in addition to the H-alpha filtergram ).

Fig.4. Singular points of the center type form a node-saddle-center group; a) the fibril structure in the neighbourhood of the sunspot of June 3, 1973 seen in the H-alpha line; b) tangential field lines form a node-saddle-center group [ by R.Loughhead, copyright C 1974 by Sol.Phys. ].
Isolated singular points of the center type, associated with a filament, are presented in the next filtergram. A filament is always associated with a current, which can emerge from below the chromosphere. In this case, the field in the vicinity of the ends of a filament is the sum of the external chromospheric magnetic field and the field created by the filament current. Such a structure can be seen in the presented filtergram. A system of retiring fibrils is visible, which form the center point in the vicinity of the end of the filament.
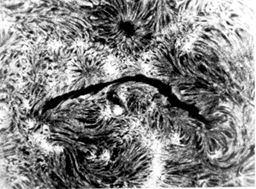
Fig.5. Singular point of the center type in the vicinity of the ends of a filament. The field lines form a system of nested closed fibril structures, that corresponds to the neighbourhood of the center-type singular point and reveal passing the current through the filament. [ by the courtesy of V.I.Makarov, Pulkovo, Russia ].
Distribution of the fibrils near the singular points can be used as a clear illustration of the theory of ordinary differential equations.
References:
Petrovsky I.G.- Lectures on the Theory of Ordinary Differential Equations, M: Nauka, 1970.
Molodensky M.M., Syrovatsky S.I.- 1979, Astronomicheskii Zhurnal, 54, 1293.
Molodensky M.M., Starkova L.I. and Filippov B.P.- 1990, Astronomicheskii Zhurnal, 67, 622-629.
Molodensky M.M. and Starkova L.I.- 1990, Astronomicheskii Zhurnal, 67, 1309-1314.
Molodensky M.M., Starkova L.I. and Filippov B.P.- 1991, Astronomicheskii Zhurnal, 68, 612-623.